Killing Fields

by Himanshu Damle

Let κa be a smooth field on our background spacetime (M, gab). κa is said to be a Killing field if its associated local flow maps Γs are all isometries or, equivalently, if £κ gab = 0. The latter condition can also be expressed as ∇(aκb) = 0.

Any number of standard symmetry conditions—local versions of them, at least can be cast as claims about the existence of Killing fields. Local, because killing fields need not be complete, and their associated flow maps need not be defined globally.

(M, gab) is stationary if it has a Killing field that is everywhere timelike.

(M, gab) is static if it has a Killing field that is everywhere timelike and locally hypersurface orthogonal.
​
(M, gab) is homogeneous if its Killing fields, at every point of M, span the tangent space.

In a stationary spacetime there is, at least locally, a “timelike flow” that preserves all spacetime distances. But the flow can exhibit rotation. Think of a whirlpool. It is the latter possibility that is ruled out when one passes to a static spacetime. For example, Gödel spacetime, is stationary but not static.

Let κa be a Killing field in an arbitrary spacetime (M, gab) (not necessarily Minkowski spacetime), and let γ : I → M be a smooth, future-directed, timelike curve, with unit tangent field ξa. We take its image to represent the worldline of a point particle with mass m > 0. Consider the quantity J = (Paκa), where Pa = mξa is the four-momentum of the particle. It certainly need not be constant on γ[I]. But it will be if γ is a geodesic. For in that case, ξn∇nξa = 0 and hence.

ξn∇nJ = m(κa ξn∇nξa + ξnξa ∇nκa) = mξnξa ∇(nκa) = 0

Thus, J is constant along the worldlines of free particles of positive mass. We refer to J as the conserved quantity associated with κa. If κa is timelike, we call J the energy of the particle (associated with κa). If it is spacelike, and if its associated flow maps resemble translations, we call J the linear momentum of the particle (associated with κa). Finally, if κa is spacelike, and if its associated flow maps resemble rotations, then we call J the angular momentum of the particle (associated with κa).
​
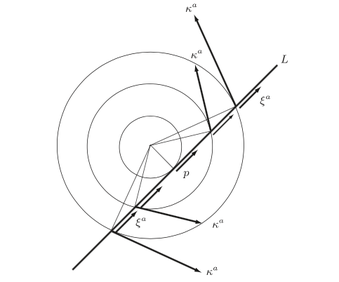
It is useful to keep in mind a certain picture that helps one “see” why the angular momentum of free particles (to take that example) is conserved. It involves an analogue of angular momentum in Euclidean plane geometry. Figure below shows a rotational Killing field κa in the Euclidean plane, the image of a geodesic (i.e., a line) L, and the tangent field ξa to the geodesic. Consider the quantity J = ξaκa, i.e., the inner product of ξa with κa – along L, and we can better visualize the assertion.

Figure: κa is a rotational Killing field. (It is everywhere orthogonal to a circle radius, and is proportional to it in length.) ξa is a tangent vector field of constant length on the line L. The inner product between them is constant. (Equivalently, the length of the projection of κa onto the line is constant.)

​Let us temporarily drop indices and write κ·ξ as one would in ordinary Euclidean vector calculus (rather than ξaκa). Let p be the point on L that is closest to the center point where κ vanishes. At that point, κ is parallel to ξ. As one moves away from p along L, in either direction, the length ∥κ∥ of κ grows, but the angle ∠(κ,ξ) between the vectors increases as well. It should seem at least plausible from the picture that the length of the projection of κ onto the line is constant and, hence, that the inner product κ·ξ = cos(∠(κ , ξ )) ∥κ ∥ ∥ξ ∥ is constant.

That is how to think about the conservation of angular momentum for free particles in relativity theory. It does not matter that in the latter context we are dealing with a Lorentzian metric and allowing for curvature. The claim is still that a certain inner product of vector fields remains constant along a geodesic, and we can still think of that constancy as arising from a compensatory balance of two factors.

Let us now turn to the second type of conserved quantity, the one that is an attribute of extended bodies. Let κa be an arbitrary Killing field, and let Tab be the energy-momentum field associated with some matter field. Assume it satisfies the conservation condition (∇aTab = 0). Then (Tabκb) is divergence free:

∇a(Tabκb) = κb∇aTab + Tab∇aκb = Tab∇(aκb) = 0

(The second equality follows from the conservation condition and the symmetry of Tab; the third follows from the fact that κa is a Killing field.) It is natural, then, to apply Stokes’s theorem to the vector field (Tabκb). Consider a bounded system with aggregate energy-momentum field Tab in an otherwise empty universe. Then there exists a (possibly huge) timelike world tube such that Tab vanishes outside the tube (and vanishes on its boundary).

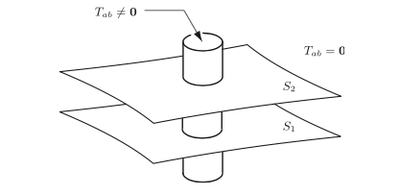
Let S1 and S2 be (non-intersecting) spacelike hypersurfaces that cut the tube as in the figure below, and let N be the segment of the tube falling between them (with boundaries included).

Figure: The integrated energy (relative to a background timelike Killing field) over the intersection of the world tube with a spacelike hypersurface is independent of the choice of hypersurface.

By Stokes’s theorem,

∫S2(Tabκb)dSa – ∫S1(Tabκb)dSa = ∫S2∩∂N(Tabκb)dSa – ∫S1∩∂N(Tabκb)dSa

= ∫∂N(Tabκb)dSa = ∫N∇a(Tabκb)dV = 0

Thus, the integral ∫S(Tabκb)dSa is independent of the choice of spacelike hypersurface S intersecting the world tube, and is, in this sense, a conserved quantity (construed as an attribute of the system confined to the tube). An “early” intersection yields the same value as a “late” one. Again, the character of the background Killing field κa determines our description of the conserved quantity in question. If κa is timelike, we take ∫S(Tabκb)dSa to be the aggregate energy of the system (associated with κa). And so forth.

One thought on “Killing Fields”

The Only Maximally Extended, Future-directed, Null and Timelike Geodesics in Gödel Spacetime are Confined to a Submanifold. Drunken Risibility. – AltExploit says:

[…] dotted circle has radius rc. Once again, that is the “critical radius” at which the rotational Killing field φa is null. Call this dotted circle the “critical circle.” The circles that pass through p and […]

altexploit